実践力の養成4
回答
重回帰分析における説明変数同士の強い相関から生じる問題のことを、「多重共線性の問題」といいます。おっしゃる通り、目安として相関係数が0.8以上のとき、多重共線性を疑います（正しくご理解されています）。Research Question1の相関行列は0.8を下回っているので大丈夫そうです。
多重共線性の問題が生じていると、決定係数がとても低くなります（当てはまりが悪くなります）。実務では、そこで「あれ？」と気が付くことがよくあります。
ご参考までですが、多重共線性を診断する指標としてVIFというものがあります。VIFが10を越えていたら多重共線性を疑いますが、私の計算では、DESIGN 2.6、FUNCTION 2.6、SIZE 2.5、PRICE 1.0で全て大丈夫でした（VIFをEXCELで計算するのは大変なので、統計分析パッケージを使いました）。
回答
もし説明変数同士の相関が強く、多重共線性の問題が生じていると考えられる場合、普通は相関の強い2つの変数のどちらかをモデルから除外します。それで決定係数やp値がある程度改善します。研究の目的にもよりますが、重回帰分析は探索的な分析なので、モデルに合わない変数を無理に残すことはありません。
じゃあ、デザインと機能のどちらの変数を残すか？なんですが、これは実際に重回帰分析を実行してみて、決定係数の良い（値の大きい）モデルの方を採用すればいいと思います。説明変数を入れ変えながら重回帰分析を段階的に繰り返し、もっとも決定係数の高くなるモデルを追求するやり方を「ステップワイズ法」といって、重回帰分析ではよく行われます。
回答
このケースだと、決定係数やp値が非常に小さい値になると思います。無理に重回帰分析にしなくても良いと思います（単回帰を試してみて下さい）。
回答
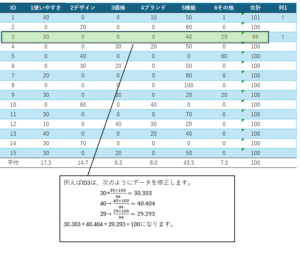
相関係数とは、変数同士一対一の関係から算出されます。例えば、機能と購買意欲の相関係数は0.87ですが、この0.87にデザインや価格やサイズなど他の変数は全く関係していません。他の変数がいくらだろうと、機能と購買意欲の相関はr=0.87です。
一方、偏回帰係数はそうではありません。ある説明変数（機能）から他の説明変数（デザイン、価格、サイズ）の影響を除いた残差変数によって、従属変数（購買意欲）を予測するものです。従って、他の説明変数の存在によって、偏回帰係数は変わってきます。機能、デザイン、価格、サイズの4つの説明変数の中で、機能が最も影響力が強いと主張したいときは、標準偏回帰係数を計算した方が説得力があると思います。ただ、偏回帰係数の計算には相関係数がかかわっているので、両者は全く無関係ではありません。
回答
私が自分でやっていることは、平均値をRの別のコマンドやEXCELでも計算してみて、間違っていないか目視で突合します。
回答
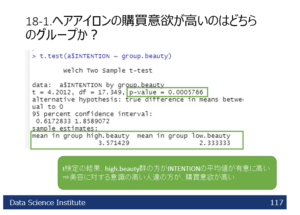
次にように書きます。
cor(a$INTENTION,d$beauty)
[1] 0.8844945
購買意欲と美容得点の相関係数は0.884で、強い相関関係がみとめられます。
