Rによる統計学（実践編）

回答

ｔ値というのは、比較したいもの同士がどれだけ違いがあるのか、
二つの比較したいもの同士の「食い違いの指標」といえます。

まず式を考えます。ｔ値の式を資料から出してみてください。
分子には比較したいもの同士を引き算していますよね？
これは、比較したい２つのうち、どちらが大きいか、または小さいかを比較する四則演算といえば引き算しかないからです。
ただ、ここで使っている数値は「平均値」を使っているので、平均値ただそれだけでは信用できないため、
信用が高い、平均値がどれだけ変動しうるのかの指標である「標準偏差」で割っています。
この辺りはＺ値を求める式と変わりません。
あとは、推測統計であるため、サンプルサイズの概念を加えています。
すなわち、比較したいもの同士、平均値での差を見つつ（分子）、平均値がどれだけ変動するかの標準偏差で割りつつ（分母）、
どれだけの個数から調べているか（サンプルサイズ）で構成されている式です。

この式を概念的に理解するならば、比較したいもの同士がどれだけ違っているかの指標と言えるかと思います。
すなわち食い違いの指標、と理解できます。
そのため、ｔ値が大きければ大きいほど、両者（比較したいもの同士）の違い（差）が大きいこととなります。
結果、両者に違いがある！という判断が間違っているかもしれない可能性（Ｐ値）は低くなっていきます。
なぜならば、両者の違いが大きい！とｔ値が教えてくれているからです。

補足ですが、このときｔ値が「+」なのか「-」なのかは重要ではありません。
なぜならば、引き算する順番で符号がプラスになったり、マイナスになったりするからです。
たとえば、t.test(a$列名１, a$列名２)であるとき、この列名１と２，左と右を入れ替えてみてください。
算出されるｔ値は符号だけ変わります。単純に左から右を引き算して、あとは割り算と掛け算しているので、
分子がマイナスになるか、プラスになるかで、ｔ値の符号が決まっているだけです。

もしまだ混乱することがございましたら、お気軽にお聞きください。

回答

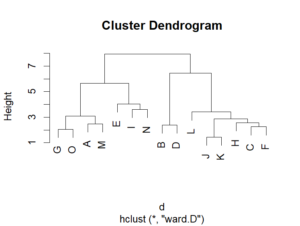
素晴らしい質問です。さて、講義で使用したのは下図でした。

これを3つとするか、4つとするかですが、これに基準はありません。
このデータはかなり綺麗ですので、縦軸にある距離がかなり近いものとなっています。
そのため、正直どこで切手も良いようには思います。
ただ、JとKが繋がるのが約1.5程度ですので、その5倍の約7の距離となると、遠いように思います。
すなわち、ここでの考えは最も近いつながりの距離と比較して、何倍程度遠いのか、という考え方がまず一つの考え方です。

続いて、たとえば、講義で使用したデータで主成分分析2のシートの新卒さんたちの試験結果でクラスター分析をしてみましょう。
下図の通りとなりました。
見てお分かりの通り、縦軸1000もあります。
とても遠い距離で、左右の塊がつながることが分かります。
上図の距離と比較すると、下図はかなり遠い距離になるくらい、つながりが遠いことがわかります。

では、下図の場合どこでグループを分けるのが良いでしょうか。
ご自身で図を作ってみて、ズームしてみると、最初のつながりは分からないけども、4人一組になっている最も小さいかたまり（クラスター）は、25以下程度のように見えます。
暫定的に20程度の距離とすると、10倍の200は遠いように思います。
どこで切るかのもう一つの考えは、これら新卒をどのような（何人の）チームしたいかという目的で考えることです。
4人一組のチームとするならば、18～19のクラスターになるよう切ることとなるでしょう。
または8～12人程度にしたいならば、、、というように目的に応じて切る位置を変えるというのがもう一つの考えです。
どこでいくつに区切るかは私たちの分析者の考えに基づきます。

回答

例えば、エクセルのデータを格納した変数名が「a」だとして、フラグ付けをしたい列名が「abc」だとします。
一旦、それら該当する列名を別の変数に格納するのが早いです。
SCO <- a$abc
そして、このSCOを書き出すのが良いです。
write.csv(SCO,”sco.csv”)
こうすると良いかと思います。

講義では、Rの実践の、主成分分析またはクラスター分析にて、この辺りを実施しています。