Rによる共分散構造分析入門

セミナーの概要

本コースでは、事例を多く用い、各事例の分析にパス図を描きながら学びます。パス図は、多様な概念を整理し、理解・説明する事象を表現するのに適していますので、実務に大いに役立てることができます。考え方のエッセンス、分析方法，分析結果の見方について分かりやすく解説します。数値の背景にある本質を読み取る実践力の習得を目標とします。演習には、クラウド型ソフトウェア「Rviewer」を用い、受講者各自1台ずつPCを用いた実践的な演習を行いますので、受講後に実務に活用できます。（数学の知識は特に必要ありません。）

共分散構造分析の特長（メリット）

（1）パス図を使い、「見える化」することにより、理解・説明力が得られます。（2）仮説に基づいた多くのモデルを自由に作成でき、各モデルの比較・検証が可能です。（3）アンケート調査データ、売上げデータ・・・多様なデータを利用することができます。

学習内容

１．パス解析

１.１　逐次モデル (Recursive Model)

【例】加齢による動脈硬化リスクについて

(1) データ概要	ある会社の健康診断を受けた男性10名の結果(仮想データ)
(2) 変数	①年齢　　②血糖値(空腹時)　　③血圧(最高値)　　④危険度(医者による診断、5段階評価)
(3) モデル	以下のようなモデルを考える。
	「④危険度　←　②血糖値　＋　③血圧」慢性的な高血糖と高血圧により動脈硬化リスクが高まると考えられる。
	「②血糖値　←　①年齢　　③血圧　←　①年齢」血糖値、血圧共に加齢による影響を受ける。
	「③血圧　←　②血糖値」高血糖は血液がドロドロなので血圧に影響する。

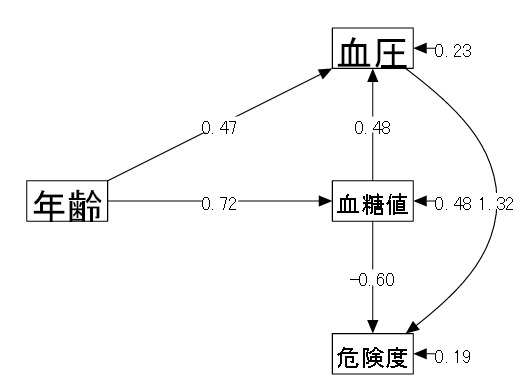加齢による動脈硬化リスクのパス図

１.２　非逐次モデル (non-Recursive Model)

【例】高校生のスマホ利用状況について

(1) データ概要	高校生100名に対して以下の調査を行った(仮想データ)
(2) 変数	①利用時間(1日の平均的な利用時間：時間) ②SNS友人(SNSでつながっている友人の数) ③会話(1日の家庭での会話時間の平均：分) ④学校友人(学校で親しくしている友人の数)
(3) モデル	以下のようなモデルを考える。
	「①利用時間　←　②SNS友人　＋　③会話」スマホ利用時間はネット上での交友関係と家庭での家族との会話の影響を受ける
	「②SNS友人　←　①利用時間　＋　④学校友人」ネット上の友人は、ネット利用時間と実生活での交友関係の影響を受ける

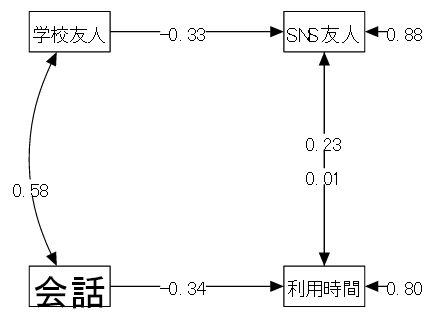高校生のスマホ利用状況のパス図

２．重回帰分析

【例】ある町におけるアパートの条件と賃貸料の関係

(1) データ概要	ある駅を最寄り駅とするアパート(間取りはほぼ同じ条件) の各種条件と問い合わせ件数(仮想データ)
(2) 変数	①賃貸料(月の賃貸料、万円) ②距離(駅からの徒歩による所要時間、分) ③築年数(年) ④問い合わせ(最近１カ月の問い合わせ件数)
(3) モデル	以下のようなモデルを考える。この例では賃貸料と問い合わせが従属変数となっているため、重回帰分析に該当する。
	「①賃貸料　←　②距離　＋　③築年数」駅からの距離と築年数によって賃貸料は変わってくる。
	「④問い合わせ　←　①賃貸料　＋　②距離　＋　③築年数」問い合わせの多さは、賃貸料と駅からの距離と築年数
	②距離と③築年数は関係ないので無相関を仮定する。

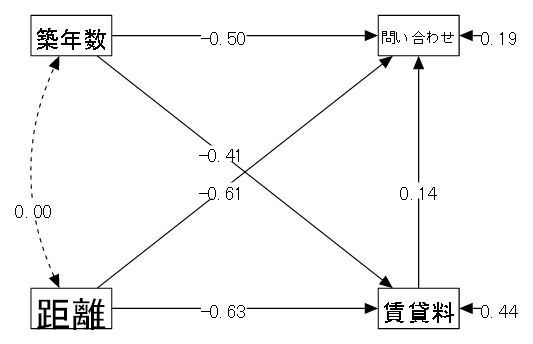アパートの条件と賃貸料、問い合わせ件数のパス図

３．MIMIC (Multiple Indicator Multiple Cause)

【例】中学生の活字離れと学業成績

(1) データ概要	中学生25名を対象に以下の調査をした(仮想データ)
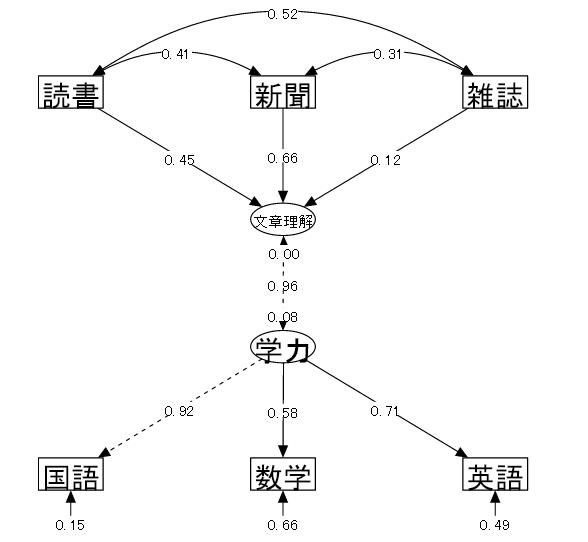
(2) 変数	①読書量(最近1ケ月の間に読んだ本の冊数) ②新聞を読む頻度(1日に新聞を読む平均時間) ③雑誌を読む頻度(1日に雑誌を読む平均時間) ④国語の成績　　　　⑤数学の成績　　　　⑥英語の成績
(3) モデル	3科目の成績から⑦学力という潜在変数を仮定し、3種の活字にふれる頻度が学力に与える影響を確認するようなモデルを立てて検証を行う。
	「⑦学力　=　④国語　＋　⑤数学　＋　⑥英語」各科目の成績から潜在変数としての学力が仮定される
	「⑦学力　←　①読書量　＋　②新聞　＋　③雑誌」学力はそれぞれの活字にふれる頻度の影響を受ける

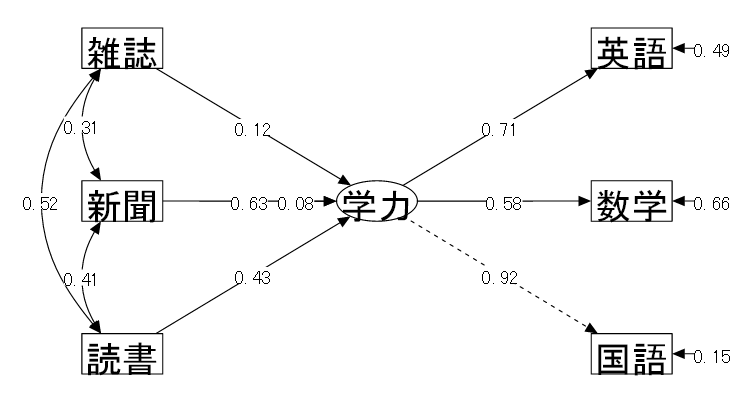MIMICモデルによる活字離れと学業成績のパス図

４．PLS (Partial Least Squares)

【例】中学生の活字離れと学業成績(仮想データ)

(1) データ概要	中学生25名を対象に以下の調査をした(仮想データ)
(2) 変数	①読書量(最近1ケ月の間に読んだ本の冊数) ②新聞を読む頻度(1日に新聞を読む平均時間) ③雑誌を読む頻度(1日に雑誌を読む平均時間) ④国語の成績　　　　⑤数学の成績　　　　⑥英語の成績
(3) モデル	MIMICの時は潜在変数を「学力」1つとし、その分析結果から仮定された「学力」は文章に関する能力と関連性が強いと想定された。そこで、もう1つ“学力"と活字にふれる頻度の間に⑧文章理解力という潜在変数を想定し、 3科目の成績から⑦学力という潜在変数を仮定し、3種の活字にふれる頻度が学力に与える影響を確認するようなモデルを立てて検証を行う。
	「⑦学力　=　④国語　＋　⑤数学　＋　⑥英語」各科目の成績から潜在変数としての「学力」が仮定される
	「⑧文章理解力　= ⑦学力」「文章理解力」は「学力」と関係がある
	「⑧文章理解力　←　①読書量　＋　②新聞　＋　③雑誌」「文章理解力」はそれぞれの活字にふれる頻度の影響を受ける
	⑧文章理解力の分散を0に指定する。
	「文章理解力」は矢印を受ける従属変数ではあるが、もう1つの潜在変数である「学力」とは異なる変数であり、モデル上では、3つの活字にふれる頻度の変数のみから表現されるものとして扱う。

PLSモデルによる活字離れと学業成績のパス図

５．2次因子分析

【例】環境問題への意識調査

(1) データ概要	100名を対象に以下の項目についての知識度を測定、7段階で評価した(仮想データ)
(2) 変数	①温暖化　　　　　②光化学スモッグ　　③酸性雨 ④レッドデータ　　⑤特定外来生物　　　⑥生態系 ⑦リユース　　　　⑧リサイクル　　　　⑨ゴミ分別
(3) モデル	大気汚染、生物多様性、ゴミの3つの問題に対する意識の高さを潜在変数として仮定し、この3潜在変数から更に2次的な潜在変数として環境問題への意識を仮定する。
	「⑩大気汚染　=　①温暖化　＋　②光化学スモッグ　＋　③酸性雨」「⑪生物多様性　=　④レッドデータ　＋　⑤特定外来生物　＋　⑥生態系」「⑫ゴミ問題　=　⑦リユース　＋　⑧リサイクル　＋　⑨ゴミ分別」「⑬環境意識　=　⑩大気汚染　＋　⑪生物多様性　＋　⑫ゴミ問題」

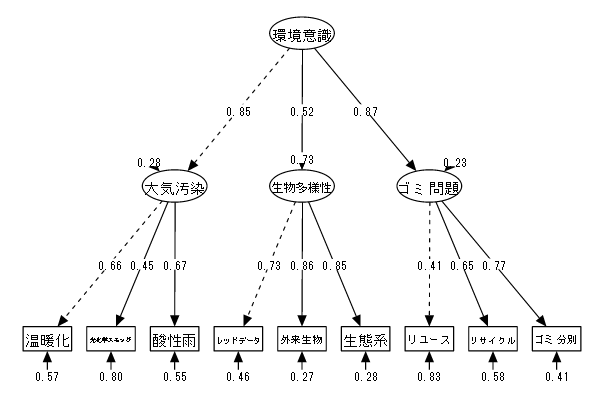2次因子分析による環境問題への意識のパス図

６．平均共分散構造分析

６.１　平均構造のあるパス解析：観測変数のみ

【例】ビールの新製品に対する評価の調査

(1) データ概要	50名のモニターに対し、以下の項目を5件法により調査した。
(2) 変数	①味満足度　　②コク　　③キレ　　④のどごし　　⑤価格　　⑥商品満足度
(3) モデル	以下の2つのモデルを仮定する。
	「①味満足度　=　②コク　＋　③キレ　＋　④のどごし」「⑥商品満足度　=　①味満足度　＋　⑤価格」

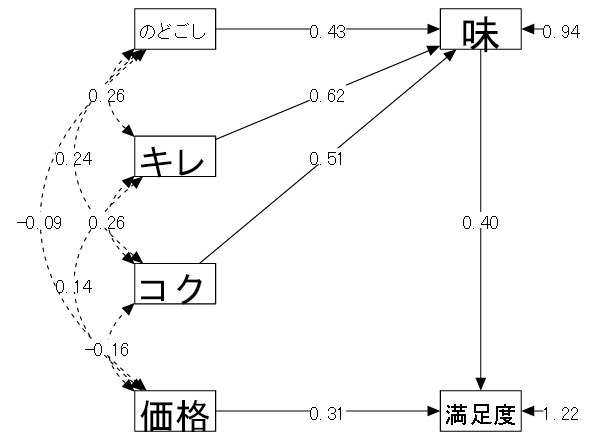ビールの新製品に対する評価のパス図

６.２　平均構造のあるパス解析：構成概念間のパス解析

【例】2次因子分析で取り上げた環境意識の調査

(1) データ概要	環境意識の知識の調査、全て7件法により評価。なお分析を簡略化するため以下の6変数に限定し、2つの因子の平均を比較する。
(2) 変数	①温暖化　　②光化学スモッグ　　③酸性雨　　④レッドデータ　　⑤特定外来生物　　　⑥生態系
(3) モデル	以下の2つの因子の比較をする。
	「⑩大気汚染　=　①温暖化　＋　②光化学スモッグ　＋　③酸性雨」「⑪生物多様性　=　④レッドデータ　＋　⑤特定外来生物　＋　⑥生態系」

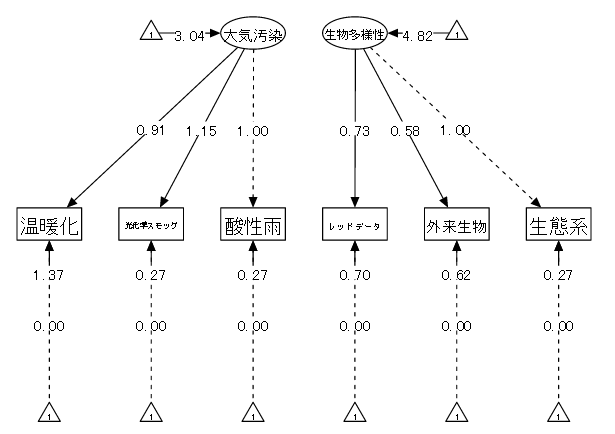温暖化と生物多様性についての共分散構造分析のパス図

７．多母集団分析：1因子の場合

７.１　配置不変モデル

【例】プロ野球の打撃成績に関する因子モデルを、パ・リーグとセ・リーグ間で比較する。モデルを簡略化するため、今回は長打力の1因子に限定し、死球の成績も追加する。

(1) データ概要	2014年のプロ野球の打撃成績(規定打席以上)
(2) 変数	①本塁打　　②打点　　③三振　　④死球
(3) モデル	4つの成績に影響する構成概念として長打力という能力を仮定し、以下のモデルをリーグ間で比較する。
	「⑤長打力　=　①本塁打　＋　②打点　＋　③三振　＋　④死球」

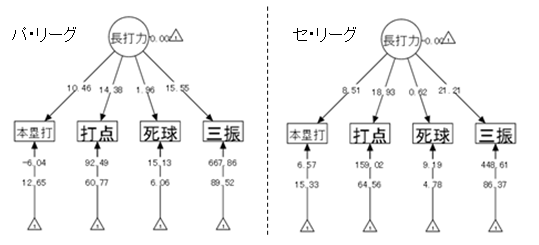打撃成績の因子モデルをリーグ間比較したパス図

７.２　等値制約に関する他のモデル

８．縦断データ分析

８.１　配置不変モデル

【例】サッカー日本代表の前監督Aと現監督Bに対する評価

(1) データ概要	日本代表サポーター50名に、以下の項目の調査を5段階評価で行った(仮想データ)。回答者は同一なため、縦断データに該当する。
(2) 変数	①人選A(前監督Aの選手選考に対する評価) ②戦術A(前監督Aの戦術に対する評価) ③内容A(前監督Aの試合内容に対する評価) ④対応A(前監督Aのマスコミ対応などの評価) ⑤人選B(現監督Bの選手選考に対する評価) ⑥戦術B(現監督Bの戦術に対する評価) ⑦内容B(現監督Bの試合内容に対する評価) ⑧対応B(現監督Bのマスコミ対応などの評価)
(3) モデル	以下のモデルを、前監督と現監督間で比較する。
	「監督の総合的能力　= 人選　＋　戦術　＋　内容　＋　対応」

８.２　等値制約に関する他のモデル

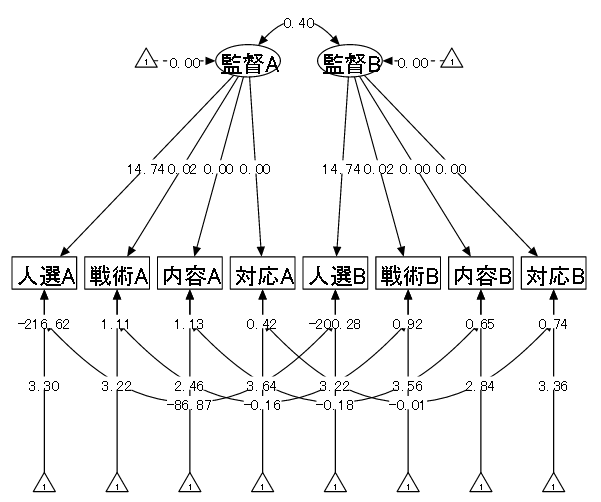弱測定不変モデルによる監督の能力評価のパス図

（セミナーの内容は変更される場合があります）セミナー終了後、希望される方には様々なご相談も可能です。

セミナーのお申し込みはこちらから