統計分析手法
記述統計
クローンバックのα係数 / 正規性の検定 / 分割表の検定
検定
【検定の種類と選択方法】
検定力分析 / ｔ検定 / 分散分析 / 比率の検定 / ノンパラメトリック検定 / 分散の検定
調査等の結果としてさまざまなデータが得られますが、データは、性別、血液型、成績順位などの質的データと、身長、売上金額などの量的データの2種類に分類されます。
またさらに、質的データは、名義尺度と順序尺度に分類され、量的データは、間隔尺度と比率尺度に分類されます。
1）名義尺度
名義尺度は、性別分類、地域別分類、(売上高の)商品カテゴリーなど、対象がもつ属性を何種類かに「分類」した尺度です。区別のみに用いられている記号ですので、数値であっても等しいか等しくないかについては意味がありますが、この数字の計算に意味はありません。
2）順序尺度
順序尺度は、成績、好みの順位など、対象間に「順序」をつけることができる尺度です。意味をもつのは順番だけですので、順序尺度の間隔の差、比などに意味はありません。
3）間隔尺度
間隔尺度は、知能指数、気温など目盛が等間隔である尺度です。絶対的な原点がありませんので、尺度間の和差には意味がありますが、比には意味はありません。
4）比率尺度
比率尺度は、身長・体重、売上高など、絶対的な原点が存在する尺度です。従って、四則演算すべてに意味があります。
記述統計
要約統計量
分散
データのバラツキの程度を表します。各データと平均値の差を二乗し合計したものを自由度で割って求めます。
標準偏差
分散の平方根です。
中央値（メディアン）
データを大きさの順に並べたときの中央にあるデータです。
切り落とし平均
データを大きさの順に並べ、上下10％の値の除いたときの平均値です。
歪度・尖度
分布が正規分布からどれだけ逸脱しているか左右対称性を示し、正規分布のときに値は0となります。分布が左にずれて裾が右に伸びているときは正の値を、右にずれて裾が左に伸びているときは負の値になります。
標準誤差
標本平均の標準偏差を指し、標準偏差を標本の大きさ（サンプルサイズ）の平方根で割ることにより求められます。
クローンバックのアルファ係数
アンケート調査などで、尺度に含まれる個々の質問項目が内的整合性を持つかどうかを判定するために用いられます。信頼性の指標となる信頼性係数のひとつで、通常、アルファ係数が0.8以上であれば一貫性があると見なされます。
正規性の検定
データの母集団が正規分布に従うかどうかについて検定します。コルモゴロフ・スミルノフ検定、及びシャピロウィルク検定を用います。
検定
検定の種類と選択方法
| 平 均 値 ・ 代 表 値 |
パラメトリック検定 | 母平均の検定 | 1標本t検定 | |
| 2群の平均値の差の検定 | 対応のない場合 | 2標本t検定 | ||
| 対応のある場合 | 対応のある2標本t検定 | |||
| 3群以上の平均値の差の検定 | 1要因対応なし | 1元配置分散分析(対応なし) | ||
| 1要因対応あり | 1元配置分散分析(対応あり) | |||
| 2要因対応なし | 2元配置分散分析(対応なし) | |||
| 2要因(1要因対応あり) | 2元配置分散分析(混合計画) | |||
| 2要因(2要因対応あり) | 2元配置分散分析(対応あり) | |||
| 各要因水準間の比較 | 多重比較 | |||
| ノンパラメトリック検定 | 2群の代表値の差の検定 | 対応のない場合 | マンホイットニのU検定 | |
| ウィルコクソンの順位和検定 | ||||
| 対応のある場合 | ウィルコクソンの符号付順位検定 | |||
| 符号検定 | ||||
| 3群以上の代表値の差の検定 | 対応のない場合 | クラスカルウォーリス検定 | ||
| 対応のある場合 | フリードマン検定 | |||
| 比率 | 母比率 | 母比率の検定 | |
| 2項検定 | |||
| 2群の比率の差 | 対応のない場合 | 比率の差の検定 | |
| フィッシャーの正確確率検定 | |||
| 対応のある場合 | マクネマー検定 | ||
| 3群以上の比率の差 | 対応のない場合 | フィッシャーの正確確率検定 | |
| 対応のある場合(2値型変数) | コクランのQ検定 | ||
| 分散比 | 2群の分散比 | F検定 |
| 3群以上の分散比 | バートレットの検定 | |
| ルービンの検定 |
ｔ検定
1標本ｔ検定（母平均の検定）
標本の平均値と与えられた値（μ）との違いについて調べます。
\[t＝ \displaystyle \frac{\overline{X}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}\]
2標本ｔ検定(対応のない場合)
2つの群のサンプルサイズ、平均値、標本標準偏差をもとに、2つの群の平均値を比較します。
2標本ｔ検定（対応のある場合）
対応のある2群のデータについて、対応するデータ間の差をもとに、差の母平均は0であるという仮説について検定します。
注）対応のあるデータ
条件を変えて同じ被験者で繰り返し反復測定したデータ。例えば、商品説明の前後に、10人について商品理解度を調べた場合、得られたデータは20ありますが10人から得られたデータですので対応のあるデータとなります。
分散分析
一元配置(対応のない場合)
3つ以上の群のサンプルサイズ、平均値、標本標準偏差をもとに、各群の平均値を比較します。平均値に違いがある場合、どの群間に差があるかを調べる場合は多重比較検定を利用します。
一元配置(対応のある場合)
乱塊法と呼ばれることもあります。
二元配置(対応のない場合)
要因が2つある場合において平均値の違いを比較します。繰り返しがない場合、交互作用はありません。 交互作用には、水準の組み合わせにより効果がさらに高くなる場合や逆に打ち消しあってしまう場合などがあります。
二元配置(混合計画)
2つの要因の内、1つの要因に、対応のある場合（同一被験者で反復してデータを測定する）に用います。
二元配置(対応あり)
2つの要因共に対応のある場合（同一被験者で反復してデータを測定する）に用います。
多重比較
分散分析の結果、全体として平均値に違いがあったときに、どの群に違いがあるのかについて調べる場合に用います。
比率の検定
母比率の検定
要約された2つの情報、データの個数と比率をもとに、母集団の比率が与えられた値（比率）と等しいかどうか検定します．
二群の比率の差の検定
母集団からサンプリングした対応のない2群のサンプルサイズと比率をもとに、2群の母集団の比率が等しいかどうかについて検定します。
マクネマー検定
対応のある2値型（2×2のクロス集計表）の2つの処理の結果に差があるかどうかを検定します
コクランのＱ検定
3つの群以上の対応のある2値型のデータにおいて、群間の比率の差の検定を行います。マクネマー検定（対応のある2群の比率の差の検定）を拡張した検定方法です。
ノンパラメトリック検定
マンホイットニのU検定
名義尺度で、対応のない2群のデータについて、2群を合わせて値の小さいデータより順位をつけ、次に2群の順位の和とデータのサンプルサイズから、統計量をそれぞれ求め、どちらか小さい方を検定統計量とし、2つのグループ間に差がないかについて検定します。
クラスカル・ウォーリス検定
名義尺度で、３群以上の対応のない場合に用いられます。バートレット検定等により分散に違いが見られた場合や、水準間でサンプルサイズに大きなバラツキがあるときには、3つ以上の平均値の違いを一元配置分散分析の代わりに、この手法を用いて検定できます。
フリードマン検定
順序尺度で、３群以上の対応のある場合に用いられます。
ウィルコクソンの検定
データに対応のない場合はウイルコクソンの順位和検定、対応のある場合はウイルコクソンの符号付順位検定を用います。
符号検定
対応のある2つの変数の組について、母代表値に違いがあるか検定します。
分散の検定
F検定
2つの群が存在するときに、各群の母分散が等しいかどうかについて検討する場合に用いられる検定です。例えば、2つの母平均の差の検定（2標本t検定）では、等分散を仮定する場合と、しない場合で検定方法が変わりますので、このような場合にもよく用いられます。
母分散の違いは、2つの群の差ではなく比を用い、F分布を利用して判断します。
バートレットの検定
2つの群の分散が等しいかどうかについて検定します。
ルビーンの検定
3つ以上の群の分散が等しいかどうかについて検定します。
分割表の検定
カイ二乗検定
分割表（クロス集計表）の各行の度数の合計と各列要素の度数の合計による比率から各セルに期待される期待度数と観測度数が等しいかどうかについて検定します。
フィッシャーの正確確率検定
分割表（クロス集計表）から独立性を検定する手法です。 組み合わせを直接計算して確率を求めます。 一般的に、カイ二乗検定による独立性の検定で、期待値が 5 以下の桝目が全体の桝目の 20% 以上あるか、期待値が 5 以下の桝目が 1 つでもある場合には、この検定手法の利用します。
相関分析
ピアソンの積率相関係数・無相関検定
2つの群に相関関係について相関係数、及び相関係数の帰無仮説を0とした無相関検定の有意確率を求めます。
相関係数（r）は次の式によって計算できます。（\(\overline{X}\)：Xの平均 \(\overline{Y}\)：Y の平均）
\[r＝ \displaystyle \frac{\displaystyle \frac{1}{N}\sum_{i=1}^{N}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sqrt{\displaystyle \frac{1}{N}\sum_{i=1}^{N}(X_{i}-\overline{X})^2}\sqrt{\displaystyle \frac{1}{N}\sum_{i=1}^{N}(Y_{i}-\overline{Y})^2}}\]
分母は、X 、Y それぞれの標準偏差の積になっていますが、分子の部分は共分散と呼ばれ、相関関係の強さを表します。
スピアマン、ケンドールの順位相関係数
2つの群に相関関係について順位相関係数求めます。スピアマン及びケンドールの方法があります。
偏相関係数
3つ以上の相関関係について、1つ以上の変数の影響を除いた相関係数です。例えば、変数X、Y、Zがあるとき、変数Zの影響を除いたXとYの相関係数です。
回帰分析
線形回帰
1個の従属変数（目的変数）と1つ以上の独立変数（説明変数）との間に式をあてはめ、従属変数が独立変数によってどの程度影響されるのかについて分析します。
商品の広告費\(x\)と売上高\(y\)、家計における収入\(x\)と食費\(y\)などの関係を調べると、\(x\)の値が変わるとそれに伴って\(y\)の値も変わるという関係がしばしばみられます。このようにある変数\(y\)とそれに影響を与えると考えられる変数\(x\)の間の関係式を求め、それに基づいての予測、及び変数の影響の大きさを評価する場合等に用いられる分析を回帰分析と言います。
この場合の変数\(y\)を従属変数（目的変数）、変数\(x\)を独立変数（説明変数）と言います。
回帰式は次のとおりです。
\( y=a+b_{1}x_{1} + b_{2}x_{2} + ・・・+b_{k}x_{k}\) （独立変数\(k\)個）
\(a\), \(b_{1}\), \(b_{2}\), ・・・の値を偏回帰係数と言い、係数の値は最小２乗法によって求めます。
＜最小２乗法＞
観察されたデータ\((x,y)\)に最もよくあてはまる直線を回帰線 \(y=a+bx\) とするとき、このデータと回帰線のバラツキが、全体としてできるだけ小さくなるような直線を考えるのが自然です。
このあてはめの方法としてよく使われている方法に最小２乗法があります。あてはめられた直線と観察点との\(y\)軸にそって、縦に測った距離の２乗和（\( \sum_{}^{}d^2\) ）が最小になるように、偏回帰係数の値を定めます。
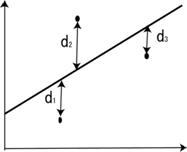\( \sum_{}^{}d^2=d_{1}^2 + d_{2}^2 + d_{3}^2 +\)・・・
＜偏回帰係数＞
独立変数の係数を偏回帰係数と言います。独立変数は従属変数を説明していますので、偏回帰係数は従属変数に対して独立変数の影響力の強さを示す値です。
従って、大きい偏回帰係数をもつ独立変数は、強く従属変数に影響を与え、偏回帰係数が小さい独立変数は、あまり従属変数に影響を与えないと言えますが、偏回帰係数の大きさは、独立変数の測定単位に影響されますので、単純な偏回帰係数相互の大小比較は意味がありません。
＜標準化偏回帰係数＞
偏回帰係数を標準化した値を標準化偏回帰係数と呼びます。標準化することにより偏回帰係数相互の比較が可能となります。
＜偏回帰係数のt検定＞
偏回帰係数については、それぞれについて有意性の検定を行うことができます。これは得られた偏回帰係数が0であるという仮説（帰無仮説）に対する検定、言いかえれば、偏回帰係数が0である確率を求めます。そして、その値が、一般的には1％または5％以下であれば、得られた偏回帰係数は0ではない、すなわち、有意（意味のあること）になります。
＜決定係数（\(R^2\)）＞
決定係数（（\(R^2\)）は、独立変数が従属変数をどのくらい説明できるかを示す指標であり、「○○％説明できる」と解釈でき、一般に、この値が高いほど、回帰分析の予側の精度が高いことになります。
決定係数（（\(R^2\)）の評価については、一般的に0.5未満：良くない、0.5以上：やや良い、0.8以上：非常に良いと言われていますが、具体的に用いる領域によって分析者の判断に委ねられます。
＜分散分析（F値）による検定＞
求められた偏回帰係数がすべて0であるという仮説（帰無仮説）に対する検定を行うことができます。従属変数の変動を回帰平方和と残差平方和に分解し、分散比（F値）を求めて検定します。一般的には1％または5％の有意確率で、仮説が正しい（採択）かどうか判断することになります。
仮説が正しい場合は、回帰分析を行うことは不適切であるという結論となります。仮説が否定（棄却）された場合は、独立変数は役に立つことになりますが、すべての独立変数が役に立つということではありませんので、それぞれの偏回帰係数についてt検定等を行い検討する必要があります。
クックのＤ統計量（クックの距離）
クックの距離は、回帰分析における影響度が大きいデータの検出などに多く用いられており、全てデータ用いた場合と１つのデータを除いた後求めた回帰式による予測値を用いた場合との食い違いに関する距離の測度です。
この距離が大きいとそのデータが回帰式による予測値に大きく影響していることを意味しますので、クックの距離が大きいデータは異常値である可能性があります。また、一般に、距離は0.5以上であれば大きいとされます。
ＱＱプロット
Q-Qプロットとは，同一の母集団から異なる二つの標本があるとき、または一方が理論分布のとき、両者のデータの分位点を対応させて、散布図にプロットしたものです。散布図上の点が直線上のとき両者は同一の母集団からの標本とみなし、そうでなければ母集団の分布が違うとみなします。
てこ比と残差
てこ比は、ある観測値が外れ値であるかどうかを判断するための指標です。てこ比が大きいデータは回帰モデルに対して大きな影響を与えます。明らかに大きいテコ比をもつデータは外れ値である可能性が高いため、必要であれば取り除きます。残差は、予測値と観測値の差（食い違い）を表します。
ロジスティック回帰
従属変数が２値（0、1）の場合、従属変数（目的変数）と1つ以上の独立変数（説明変数）との間に式をあてはめ、従属変数が独立変数によってどの程度影響されるのかについて分析します。
非線形回帰
回帰分析において、従属変数と独立変数が非線形の場合に用います。非線形モデルは、線形モデルよりも指定や推定が困難で、回帰モデル式を選択し、パラメータの初期値を指定する必要があります。モデルによってはうまく当てはまらないものもあります。
ステップワイズ法
線形回帰において、最適な独立変数の数を設定し回帰式を求めます。独立変数の選択には、増加法、増減法、減少法の3通りがあります。また、選択の基準に、赤池情報基準（AIC）が用いられます。
一般化線形モデル
正規分布以外のモデルに対応するために、分布（正規、二項、ガンマ、疑似尤度二項、疑似尤度ポアソン、疑似尤度、逆正規）を用いた回帰分析です。
多変量解析
主成分分析
主成分分析は、多数の変量の間の相関関係に着目し変量に共通する要素を抽出するための分析方法です。
＜主成分負荷量＞
主成分負荷量は、その主成分が何を表しているかを解釈するときの手がかりとなります。
＜寄与率、累積寄与率＞
寄与率は、各主成分がそれぞれ受けもって表現している情報量を比率で表現したものです。例えば、第１主成分の値が0.6の場合、これは第１主成分が全情報量の60％を集約して表現していることを意味します。
累積寄与率は、この寄与率を順番に加算し求められ、最大値は100％となります。
因子分析
因子分析とは、複数の項目間に共通して作用する潜在的な要因を探し出そうとする分析です。言いかえれば、相互の関連を数個の因子で説明しようとする分析です。
＜因子の抽出方法＞
因子の抽出方法には、主因子法、最尤法、主因子法、一般最小二乗法、重み付き最小二乗法、残差最小法等があります。最近は、コンピュータ性能の向上と共に、最尤法がよく利用されるようになりました。
最尤法は洗練された方法ですが、実際のデータの正規性（正規分布であること）が求められます。正規性が認められない場合は、主因子法の利用が無難と言えます。
主因子法（反復主因子法）は、重相関係数の２乗を共通性の推定値として用いて、因子寄与を繰り返して収束するまで計算する方法です。第一因子の因子寄与が最も大きくなるという特徴があります。
最尤法は、変数の単位を変えても、因子構造は変わらないという特徴がありますが、解が収束しなかったり、共通性が1を超えてしまうなどの問題もよく起こります。
＜因子数の決定＞
因子分析を、回転をかけずに行うと、初期解（最初の結果）が求められます。
初期解で得られた因子から、因子数を決めなければなりません。因子を選ぶ方法には、固有値の値（回転前の因子寄与）が1以上とするカイザーガットマン基準と呼ばれる方法、固有値の落差の大きいところで決めるスクリープロット基準などの方法があります。どちらの方法もよく使われます。
＜回転＞
回転には、直交回転と斜交回転があり、回転することにより因子分析の結果が解釈しやすくなります。
直交回転
直交回転、すなわち、二つの因子の軸が直交（90度）を保ったままの回転の代表的な方法で、バリマックス回転がよく用いられます。この直交回転でできるだけ因子負荷を「単純構造」に近づけるよう回転します。
斜交回転
直交回転は、二つの因子の軸が直交（90度）を保ったままの回転でしたが、斜交回転は、90度ではありません。二つの因子の相関関係が無い場合には二つの軸は直交しますが、相関関係がある場合は、二つの軸は直交しません。直交回転は因子間の相関が無いという仮定において行われる回転ですが、斜交回転は逆に因子間に相関があるものとして解を出します。
従って、直交回転は、二つの軸を同時に動かしましたが、斜交回転は、二つの軸を個々に動かし、単純構造を目指します。当然、直交回転より単純構造になりやすくなります。 斜交回転の方法には、プロマックス、オブリミン、シンプリマックス、クオーティミン等 があります。
＜因子負荷量＞
因子負荷量とは、各因子と各質問項目の関連の度合い（関連性）です。
＜因子寄与率、累積寄与率＞
因子負荷量が高い因子がみつかるということは、因子と質問項目との関連性が成立していることになります。言いかえれば、因子負荷量が高いものがたくさんあれば、項目が因子を説明するのに寄与しているという言い方もできます。そこで、因子寄与という言い方がされ、寄与が高いまたは低いという言い方がされます。
因子寄与がどの程度あるかは、因子負荷量で把握できます。各因子の因子負荷量が高ければ、その分各質問項目がその因子を説明するのに寄与していると言えます。
因子の寄与の程度は、因子負荷量を縦方向に合計しますが、因子負荷量には負の値もありますので、単純合計ではなく、２乗して合計、すなわち、因子負荷量の２乗和を計算します。この値を「因子寄与」と言い、求めた因子寄与を因子寄与の最大値である質問項目の数で割り、寄与率が求められます。
累積寄与率は、この寄与率を順番に加算し求められ、最大値は100％ですので、抽出された因子全体として、どの程度寄与しているかみることができます。
＜共通性＞
因子寄与、寄与率は、因子に着目した場合ですが、各質問項目に着目してみます。
質問項目は、共通因子を探るために設けますが、共通因子を反映しない質問項目が出てくることもよくあります。それをみるために、各質問項目の因子負荷量を横方向に合計しますが、因子寄与の場合と同じように各値を２乗して合計します。この値を共通性と言います。
共通性は、その言葉どおり、共通因子の部分がどの程度であるのかについて示す指標です。共通性は、原則的に最大値が1ですので、共通性の各値を見ていくと、それぞれの質問項目が共通因子を探り出すのにどの程度役立っているのか分かり、共通性を合計すると因子寄与の合計と等しくなります。
＜因子得点＞
因子分析によって因子を抽出した後に、各評定者がそれぞれの刺激をどの程度評価していたのかについて表したものが因子得点です。従って、因子得点は各回答者別に算出されます。一人ひとりの回答者に対して、第1因子得点○○点、第2因子得点○○点…と算出されます。因子得点の算出方法には、回帰による方法、他バートレット等があります。
クラスター分析
階層的クラスター分析
距離や相関係数によって、ケースの類似度を求め、類似度の近い順にグループ化を行います。最初はケースの数だけクラスターがありますが、結合するたびに減っていきます。ラスター分析とは、異なる性質のものが混ざりあっている集団（対象）の中から互いに似たものを集めて集落（クラスター）を作り、対象を分類しようという方法を総称したものです。
このクラスター分析を用いると客観的な基準に従って科学的に分類ができるため、心理学、社会学、認知科学からマーケティングなど様々な分野で用いられます。
クラスター分析は大きく、階層的手法と、非階層的手法に分けられ、階層的手法は、さらに凝集型と分岐型に分けられますが、ここでは、よく使用される階層的手法の凝集型について説明します．
具体的な手順は、最初に類似性の定義を行って、サンプル間それぞれの距離を算出し、それに応じてサンプル同士をまとめ（クラスタリング）、樹形図（デンドログラム）などで視覚化します。
クラスタリングの方法も、分析や用途に応じてさまざまなものが提唱され、その分類もいろいろありますが、階層的方法には、ウォード法、最短距離法、最長距離法、メディアン法、重心法、群平均法等があり、距離を求める方法にも、ユークリッド、マンハッタン、最長、ミンコフスキー、キャンベラ、バイナリー等の」方法があり、データの性質とグループ分けするための方針により使い分けします。
非階層的クラスター分析
階層的な構造を持たず、あらかじめいくつのクラスターに分けるかを決め、決めた数のクラスターにサンプルを分割する方法です。 階層クラスター分析と違い、サンプル数が大きいデータを分析するときに適しています。 アルゴリズムには、Hartigan-Wong、Loyd、Forgy、MacQueeen等があります。
判別分析
あらかじめどのサンプルがどの群に属するかというデータをもとに、どの群に属するか分からないサンプルがどの群に属するのかを判別する関数を求め、各データがどの群に所属するかを判定します。
正準相関分析
従属変数、独立変数という区別ではなく、それぞれ複数の変数からなる 2 変数群それぞれについて合成し、2 つの合成変数の相関が最も大きくなるような重みを求めます。
数量化分析
数量化Ⅰ類
質的なデータ（例 晴れ、雨）を用いた線形回帰分析です。
数量化Ⅱ類
カテゴリーデータを説明変数として群を判別します。ある商品の購入者と非購入者、広告の認知者と非認知者等、グループに分けた時、ある特性をもつ回答者がどのグループに属するかを判別する手法です。
数量化Ⅲ類
複数のデータの特徴（アンケート質問に対する回答パターン等）から、サンプル相互の距離（類似度）、カテゴリー（回答選択肢）相互の距離を得点化し、サンプルやカテゴリーの特性を分類して解釈する手法です。コレスポンデンス分析、双対尺度法と同じ結果が得られます。
数量化Ⅳ類
各項目間の近似度を求め、空間表示を行う手法です。似ているものほど近くに配置されます。
共分散構造分析
共分散構造分析（structural equation modeling; SEMともいいます）は、構成概念や観測変数の性質を調べるために集めた多くの観測変数を同時に分析するための統計的方法です。言いかえれば、回帰分析や因子分析は共分散構造分析の一部とも言え、ある変数が別の変数に影響を与えることや、ある観測変数がある潜在変数から影響を受けることなどを扱います。
生存時間分析
カプランマイヤー生存曲線
生存率曲線を描くことで生存時間の推定を行います。また、死亡発生ごとに生存率を計算するので、少数例の場合にも正確な生存率を求めることができます。
コックス比例ハザード分析
年齢や性別などの説明変数の効果を説明する生存データの分析（回帰分析）によく使われます。
一般化ウィルコクソン検定
時点ごと重みを考慮し、ハザード比（イベント発生率の比）が変わるような場合でも対応できる検定方法です。ログランク検定は2群のハザード比が一定であることを想定していますので、途中でハザード比が変わるようなデータの場合は不向きです。
ログランク検定
2つの生存曲線が同じかどうかを調べます。群ごとにイベントの有無別に集計した分割表（クロス集計表）のカイ2乗値を検定統計量として利用します。
コックス・マンテル検定
生命表のデータを対応のある2分類データと考え、繰り返しのある二元配置分散分析同様の方法により、累積生存率曲線全体を群間比較します。
箱ひげ図
箱ひげ図の構成要素には、箱の中央付近のヨコ線、箱のヨコ線、箱の上下の短いヨコ線箱の上下の短い線の外側の点があります。
箱の中央付近のヨコ線 → データの中央値
箱のヨコ線 → データの第1四分位数（下側）と第3四分位数（上側）
箱の上下の短いヨコ線 → 外れ値を除くデータの最小値（下側）・最大値（上側）
真ん中付近の赤い▽ → 平均値
緑色の上下線 → 平均値±標準偏差
（外れ値）
「第1四分位数から四分位範囲の1.5倍を引いた値を下回っているデータ」と「第3四分位数に四分位範囲の1.5倍を加えた値を超えているデータ」が外れ値として定義され、外側にプロットされます。
効果量
慣習的に、有意な差があるかについての検定は、ｔ検定や分散分析などの分析を行い、有意確率が0.05以下の場合には、有意水準5％において有意な差があったという結論としますが、この様な検定は、サンプルサイズ（サンプル数）が大きくなればなるほど、統計的に有意であるという結果になります。
効果量は、サンプルサイズによって変化することのない指標です。実験の条件によっては、有意差があっても効果量が小さい場合もあれば、有意差がなくても効果量が大きい場合も考えられるため、有意確率と共に、効果量も報告すべきであるとされます。
効果量の定義式
・2標本ｔ検定
\[Cohen’s \; d＝ \displaystyle \frac{\overline{X}_{1}-\overline{X}_{2}}{\sqrt{\displaystyle \frac{n1s1^2+n2s2^2}{n1+n2}}}\]
\[Hedges’s \; g＝ d \times
\left(1 – \displaystyle \frac{3}{4({n}_{1} – {n}_{2}) – 9}\right )\]
\[r＝\sqrt{\displaystyle \frac{t^2}{t^2+\phi}}\]
・対応のある2標本ｔ検定
\[Cohen’s \; d＝ \displaystyle \frac{\overline{X}_{1}-\overline{X}_{2}}{\sqrt{\displaystyle \frac{n1s1^2+n2s2^2}{n1+n2}}}\]
\[Hedges’s \; g＝ d \times
\left(1 – \displaystyle \frac{3}{4({n}_{1} – {n}_{2}) – 9}\right )\]
\[r＝\sqrt{\displaystyle \frac{t^2}{t^2+\phi}}\]
\[調整済み \; d＝\displaystyle \frac{\qquad Cohen’s \qquad}{\sqrt{2(1-2変量の相関係数) \qquad}}\]
\[調整済み \; g＝\displaystyle \frac{\qquad Hedges’s \qquad}{\sqrt{2(1-2変量の相関係数) \qquad}}\]
・1元配置分散分析（対応のない場合）
\[ \eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Total}} \]
\[ \omega^2=\displaystyle \frac{SS_{Effect}-φ_{Effect} \times MS_{error} }{SS_{Total}+MS_{error}} \]
\[ 偏\eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Effect}+SS_{error}} \]
\[ 偏\omega^2=\displaystyle \frac{SS_{Effect}-φ_{Effect} \times MS_{error} }{SS_{Effect}+(N-φ_{Effect}) \times MS_{error}} \]
\[f=\displaystyle \frac{母集団における平均値の標準偏差}{各群内における母集団標準偏差}\]
・1元配置分散分析（対応のある場合）
\[ \eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Total}} \]
\[ \omega^2=\displaystyle \frac{SS_{Effect}-φ_{Effect} \times MS_{error} }{SS_{Total}+MS_{error}} \]
\[ 偏\eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Effect}+SS_{error}} \]
\[ 偏\omega^2=\displaystyle \frac{SS_{Effect}-φ_{Effect} \times MS_{error} }{SS_{Effect}+(N-φ_{Effect}) \times MS_{error}} \]
\[f=\displaystyle \frac{母集団における平均値の標準偏差}{各群内における母集団標準偏差}\]
・2元配置分散分析（2要因に対応のない場合）
\[ \eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Total}} \]
\[ \omega^2=\displaystyle \frac{SS_{Effect}-φ_{Effect} \times MS_{error} }{SS_{Total}+MS_{error}} \]
\[ 偏\eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Effect}+SS_{error}} \]
\[ 偏\omega^2=\displaystyle \frac{SS_{Effect}-φ_{Effect} \times MS_{error} }{SS_{Effect}+(N-φ_{Effect}) \times MS_{error}} \]
\[f=\displaystyle \frac{母集団における平均値の標準偏差}{各群内における母集団標準偏差}\]
・2元配置分散分析（1要因に対応のある混合）
\[ \eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Total}} \]
\[ 偏\eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Effect}+SS_{error}} \]
・2元配置分散分析（2要因に対応のある場合）
\[ \eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Total}} \]
\[ 偏\eta^2=\displaystyle \frac{SS_{Effect}}{SS_{Effect}+SS_{error}} \]
・線形回帰分析
\[f^2=\displaystyle \frac{自由度調整済決定係数}{１－自由度調整済決定係数}\]
標本検定力
αを第一種の誤り、βを第二種の誤りとしたときに、帰無仮説が真のとき正しく採択される確率が1－αであり、一般的な検定によく使われます。これに対して、帰無仮説が偽のとき正しく採択される確率が1－βです。この 1－βを検定力と定義します。
αは、0.05、0.01と設定することができますが、βは、帰無仮説が偽の状況が様々あり明示的に設定できません。（従って、α+β＝1とはなりません。）
標本検定力は、サンプルサイズ、効果量、αにより求められます。また、αと検定力、効果量と検定力、及びサンプルサイズと検定力は比例します。
必要標本数
必要標本数は、効果量、設定したα、及び1－βにより求められます。
イェーツの連続性の補正（Yate’s continuity correction）
度数で表されるような離散型分布を、カイ二乗分布や正規分布などの連続型分布に近似させて統計的検定を行うときに用いる修正方法です。検出力は低下しますが、より正確な検定が可能になります。
赤池情報量基準（Akaike’s information criterion / AIC）
統計的モデルを観測値と理論値の差（残差）を用いて評価する統計量です。値が小さいほど当てはまりが良いと言えます。